In this exercise you'll learn how to inscribe 3 circles:
Needed analogue tools:
Dividers
Pencil
Straight Edge
Eraser
Given:
Circle, R=10
Desired:
3 Inscribed Circles
Note: Refer to GC-11 for circumference division and GC-02 for drawing a perpendicular line.
Divide the given circle's circumference in 6 parts (GC-11). Mark each point as shown.
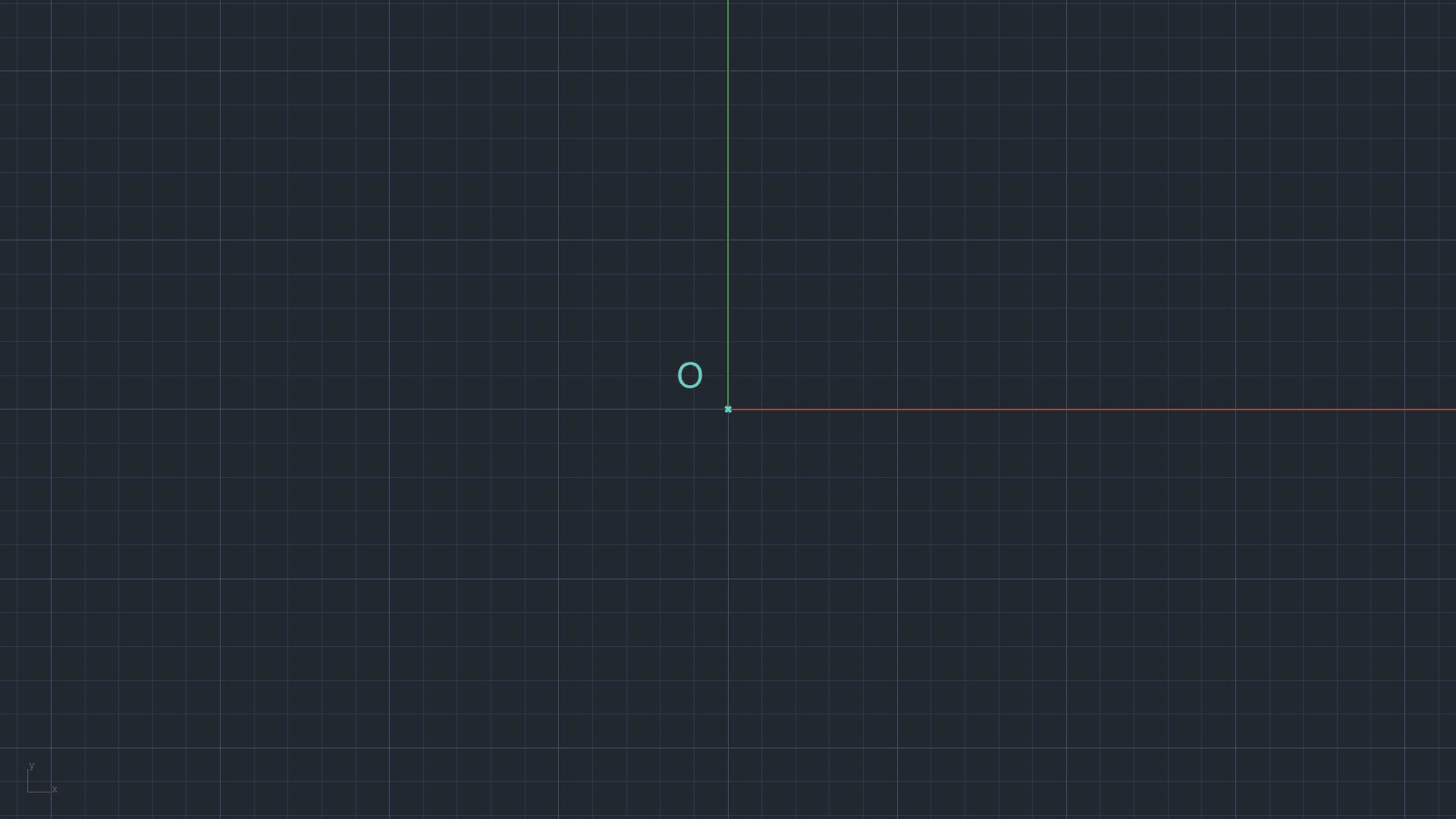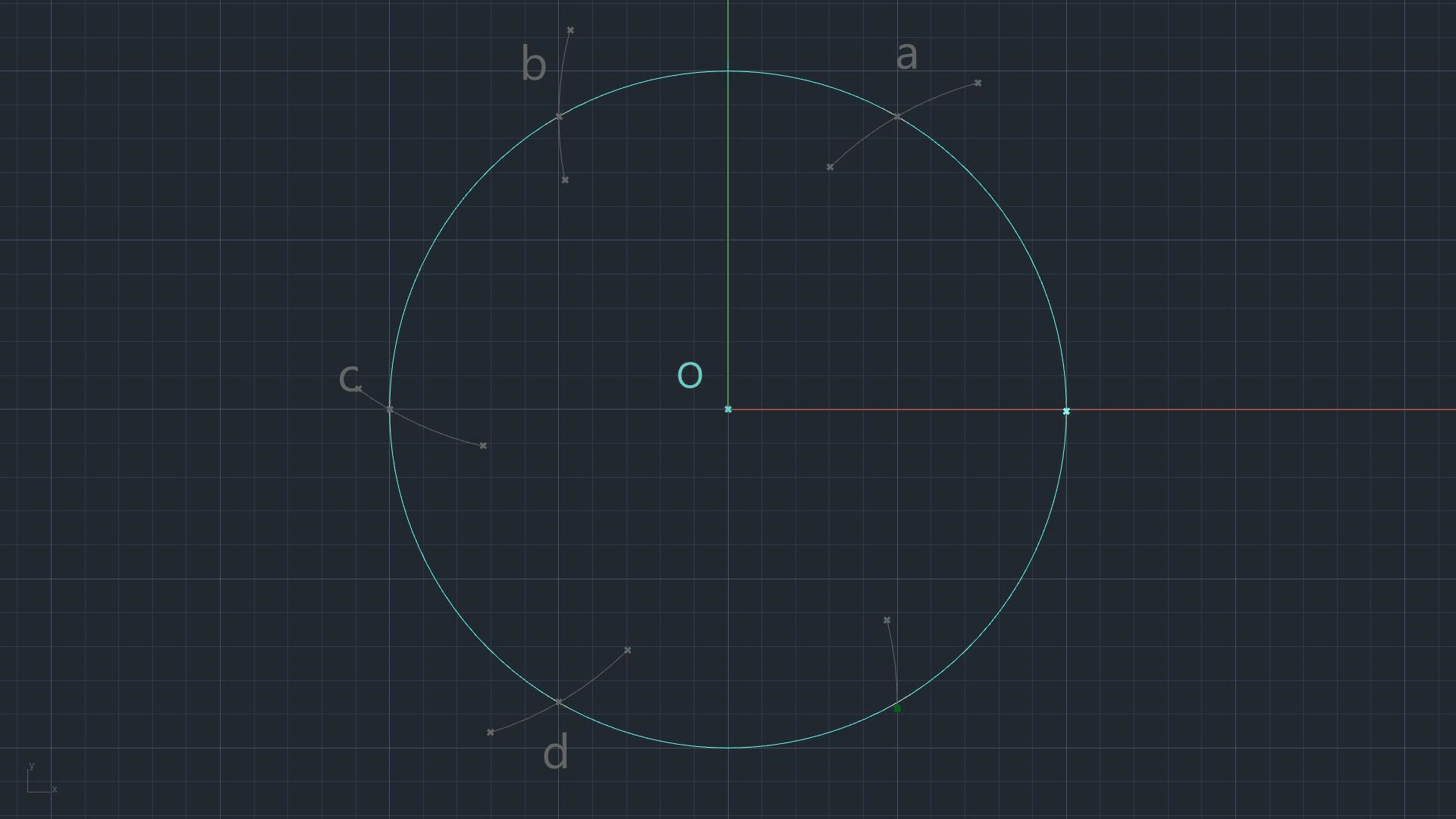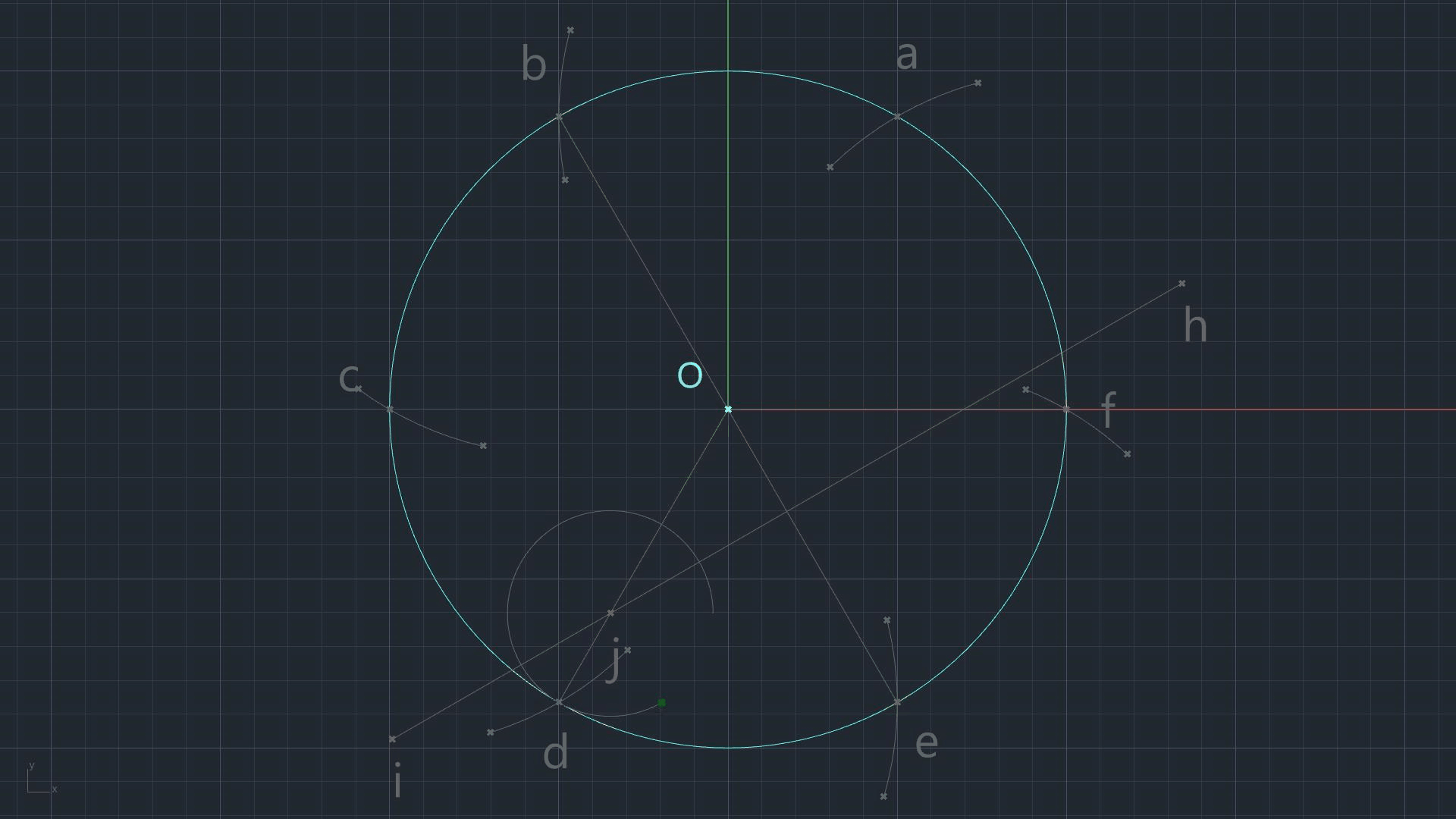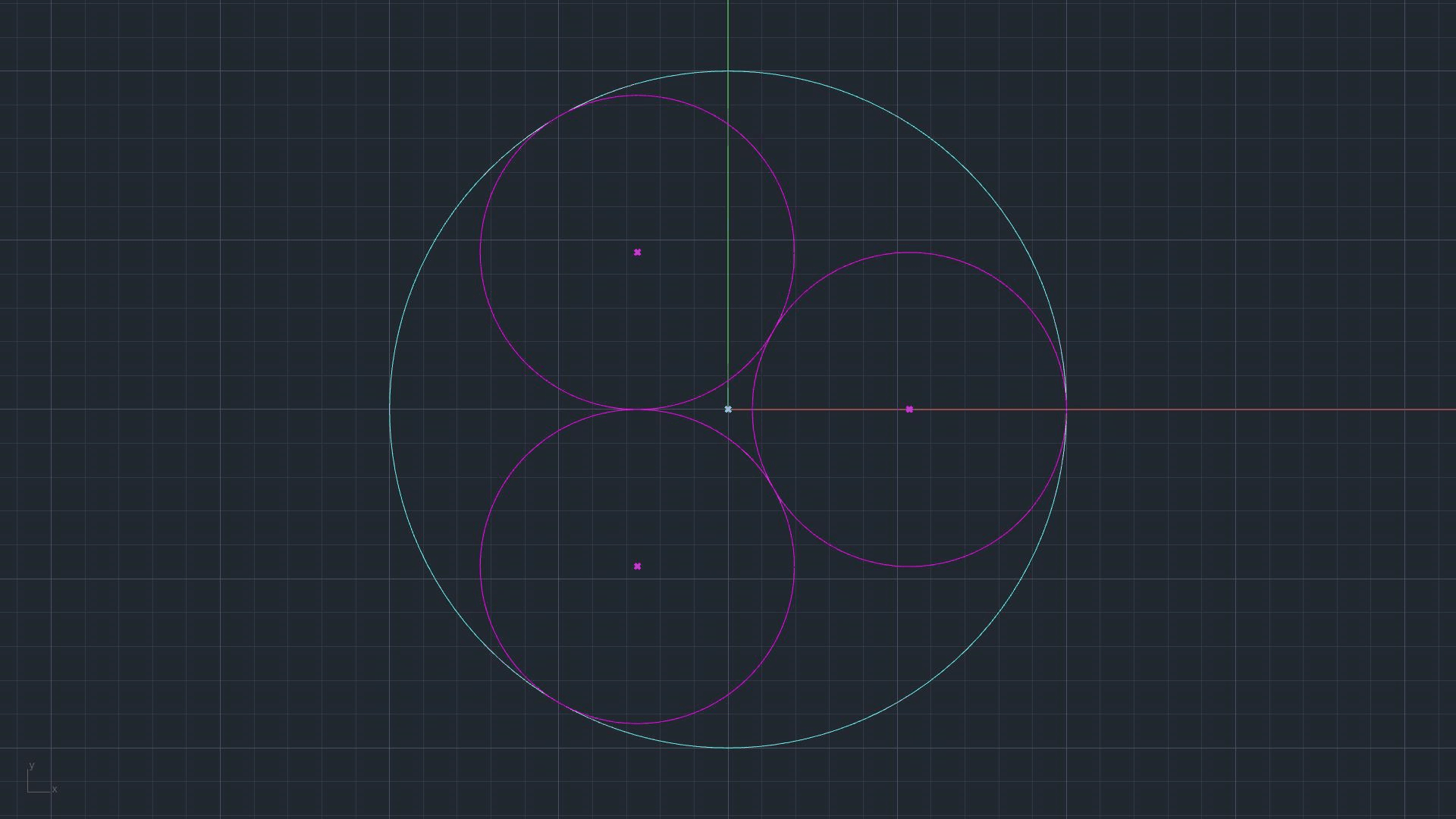
Connect f with O, b with e (passing through O), d with O.
Draw a line, h-i, perpendicular (GC-02) to b-e. The line should be drawn anywhere within the circle's area and crossing O-d.
Mark the intersection of h-i with O-d as j.
Draw a circle with center j and radius j-d.
Circle j-d intersects line h-i. Mark the intersection as k.
Connect d with k and extend the line to cross b-e.
The intersection of b-e with d-k is marked as l.
Draw another line, n-o, perpendicular to b-e, passing through l.
Line n-o crosses o-d. Mark the intersection as p.
Draw a circle with center O and radius O-p.
Mark the intersections of circle O-p with f-o and b-o as r and q. Both of which (r and q) are equivalent to p.
Draw the first inscribed circle with center r and radius r-f.
The second inscribed circle is drawn with center q and radius q-b.
Third inscribed circle - center p and radius p-d.
The order of drawing the inscribed circles is of no consequence.
You can download the CAD and GH file here:





























Kommentare