Ever wondered how the radian can be found graphically? Here's one way to do it:
Needed analogue tools:
Dividers
Pencil
Straight Edge
Eraser
Given:
Circle A-B, R=10, D/7
Desired:
Radian Angle=180°/π=57.296°
Note: Refer to GC-09 to find out how to divide a line segment.
Divide A-o in 7 equal segments. The distance from Point A to its closest point (we just created) is 1/7 of A-o, or 1/49 of A-B.
Set one leg of the dividers at O (Circle A-B's center), stretch the other to the point (Step 2) nearest to A.
Maintaining that stretch, place one leg on Point B.
Swing the other leg of the dividers across Circle A-B's circumference.
Mark the intersection.
Connect Point O (A-B's center) with the intersection point (Step 5).
Draw another line from O to B.
These two lines cut Circle A-B's circumference. The length of the arc thusly defined approximates closely that of Circle A-B's radius.
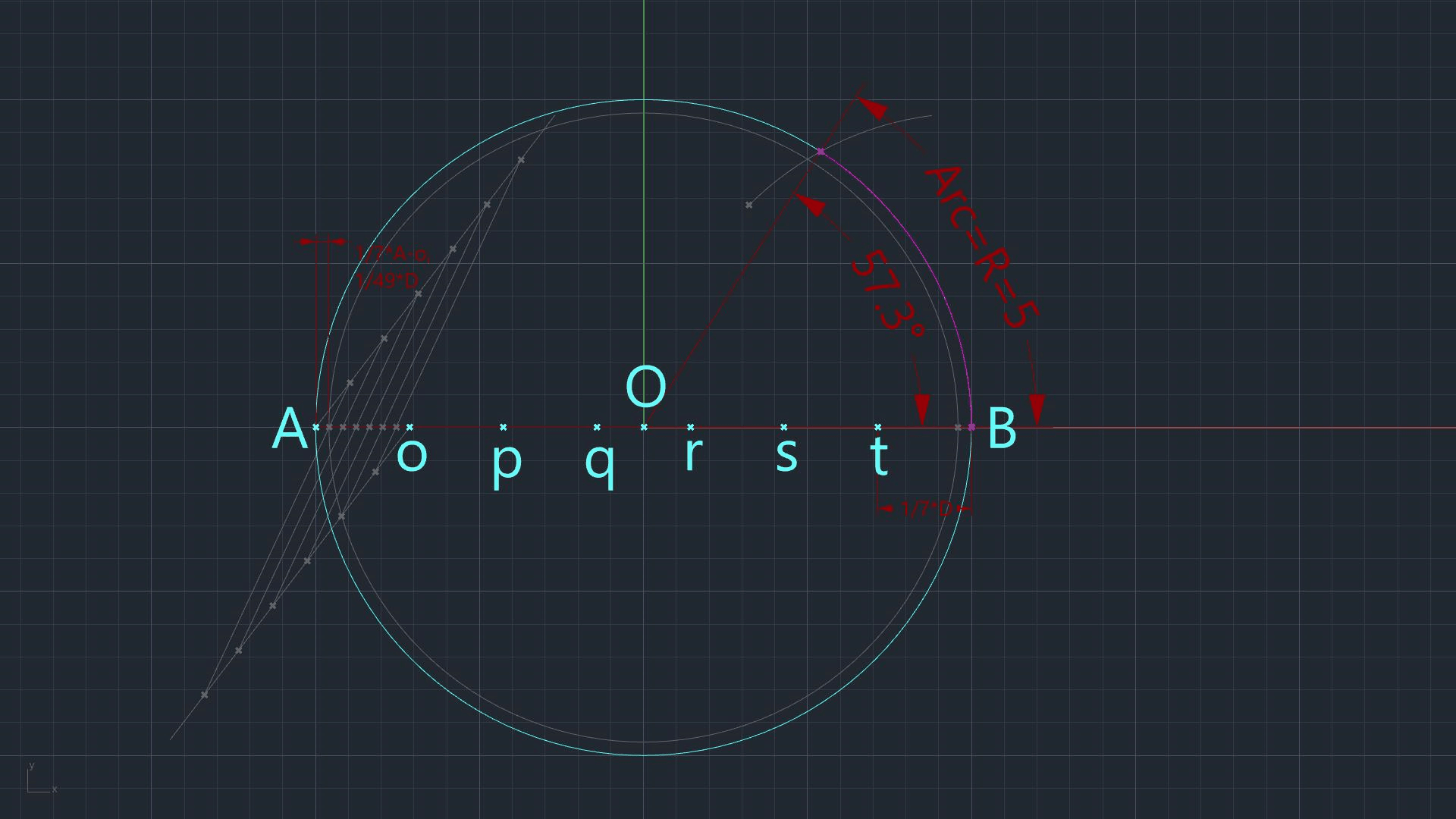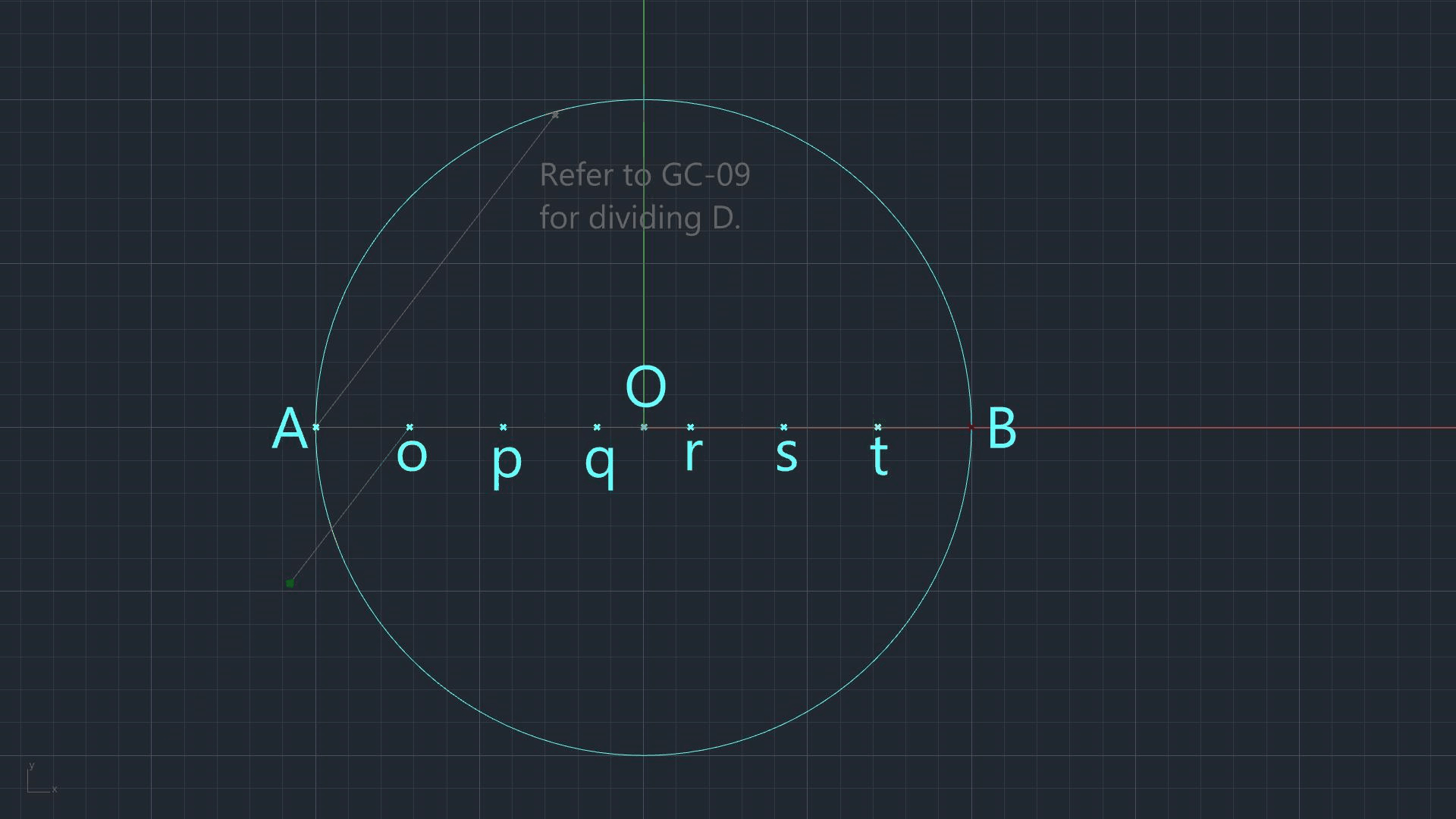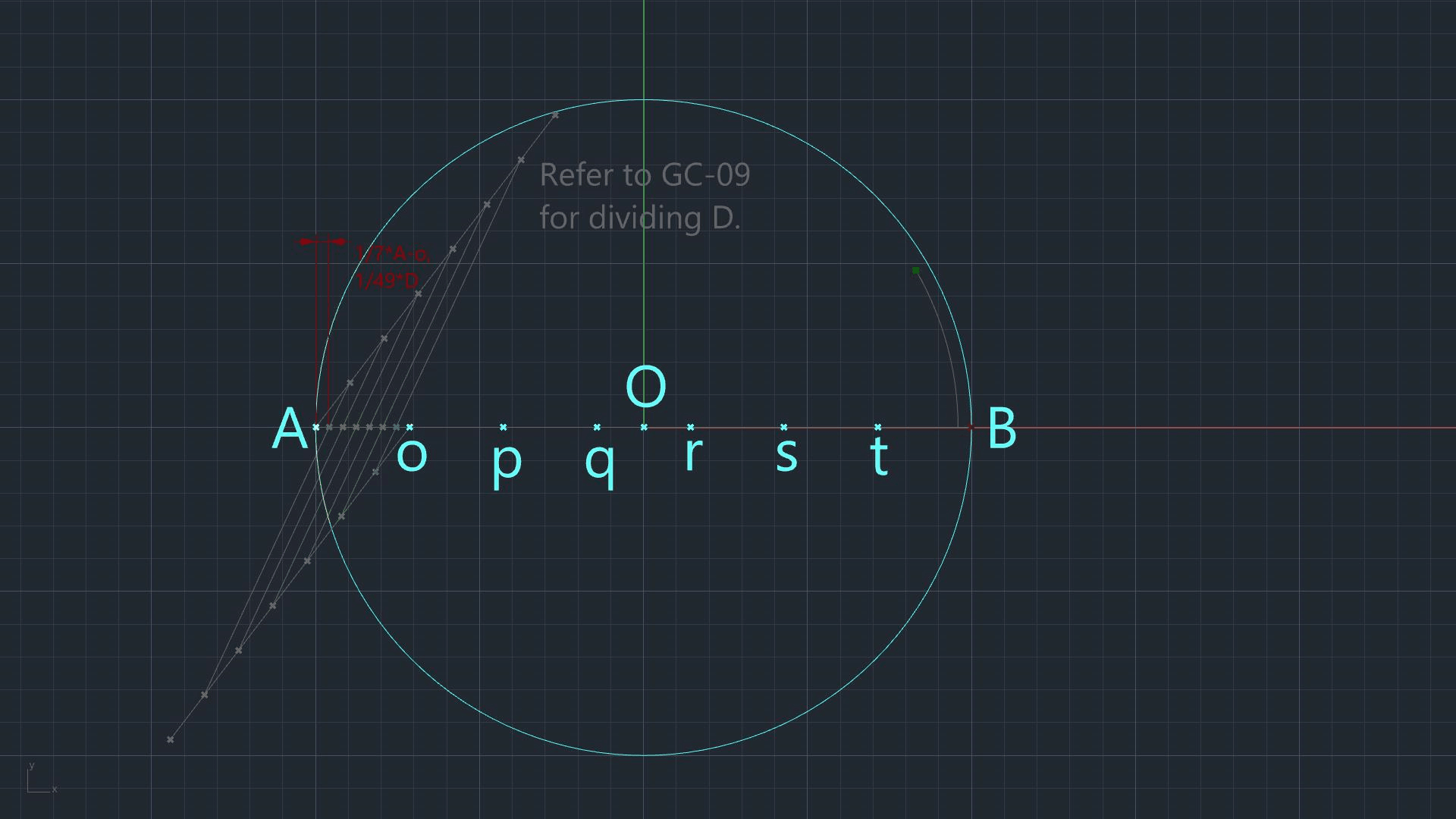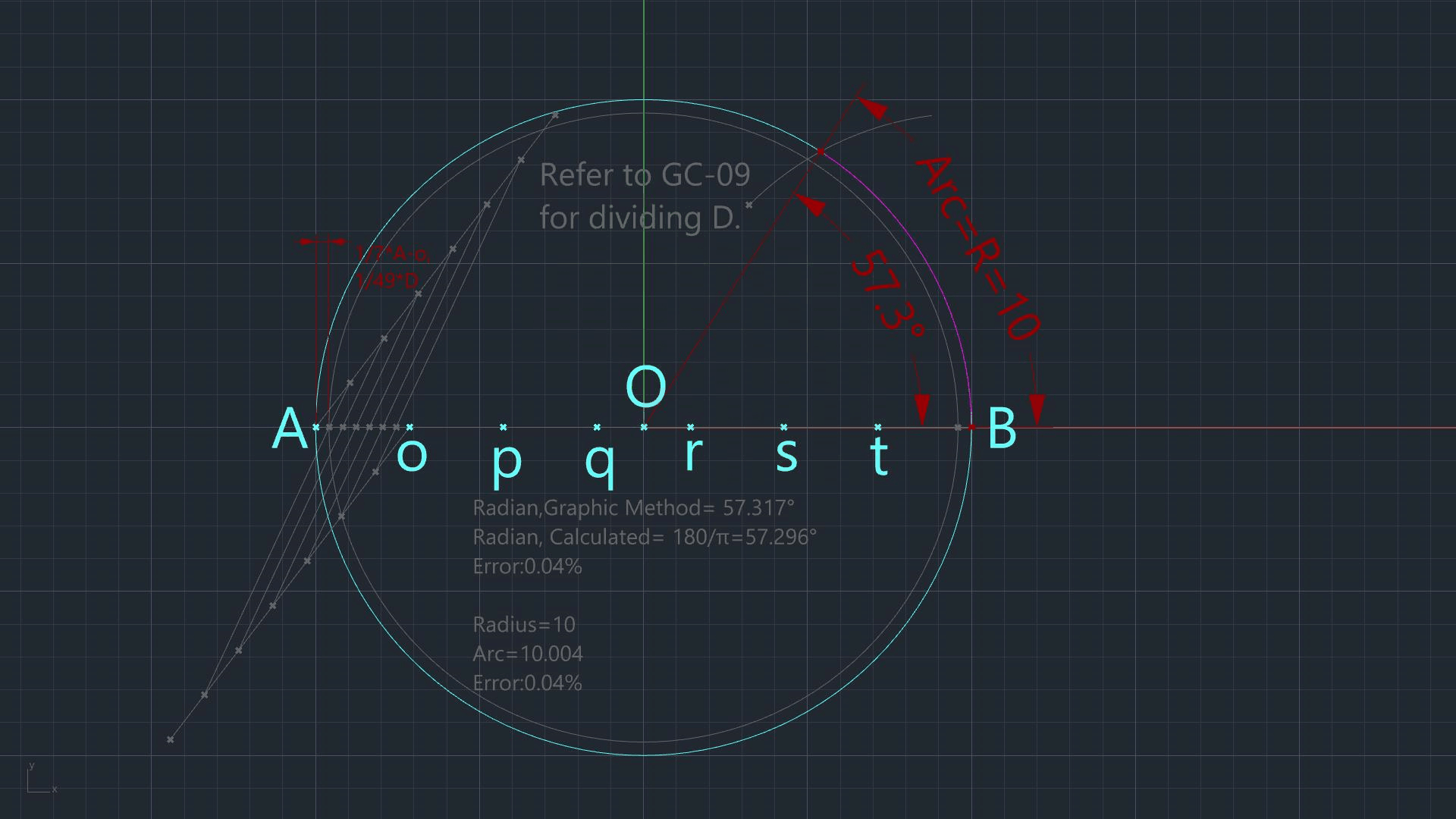
The angle subtended by the lines drawn (Step 6, 7) equals 57.317° and is called Radian.
The graphical solution described above gives the following results:
Arc's length = 10.004
Radian Angle = 57.317°
If those same parameters are calculated, the results would be:
Arc's length = 10.000
Radian Angle =180°/π=57.296° = 57.296°
That's a difference of no more than 0.04% which would be accurate enough for most common carpentry tasks.
You can download the CAD and GH file here:

























Comments